Попалась хорошая заметка с критикой тестов на нормальность. Лучше прочесть ее в оригинале, она небольшая и достаточно наглядная, но вот совсем короткое резюме:
На маленьких выборках тест очень редко отличает распределение от нормального, даже если оно заведомо ненормальное (скажем, лог-нормальное). На больших выборках, напротив, даже небольшое отклонение от нормальности приводит к отклонению гипотезы от нормальности.
Автор заметки в качестве ненормального распределения, в частности использует распределение Стьюдента с 20 степенями свободы, “на глаз” оно мало отличимо от нормального:
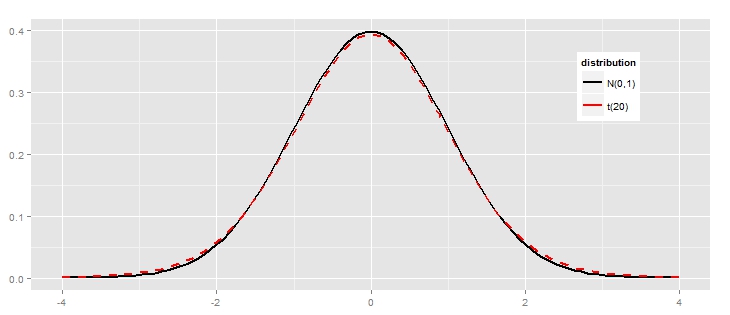
Однако, у этого распределения есть по сравнению с нормальным то, что называется “тяжелыми хвостами распределения”, что и приводит к провалу теста на нормальность. Дальше в заметке приводится пример нормального распределения со специально утяжеленными хвостами – результат сходный.
Ещё один вариант “почти нормального распределения” я нашёл в другом обсуждении на ту же тему: к стандартному нормальному распределению добавляется систематический шум, например, последовательно к каждым пяти элементам прибавляется вектор (1, 0, 2, 0, 1), в r это выглядит так: rnorm(1000)+c(1,0,2,0,1). Получаемое распределение тоже похоже на нормальное:
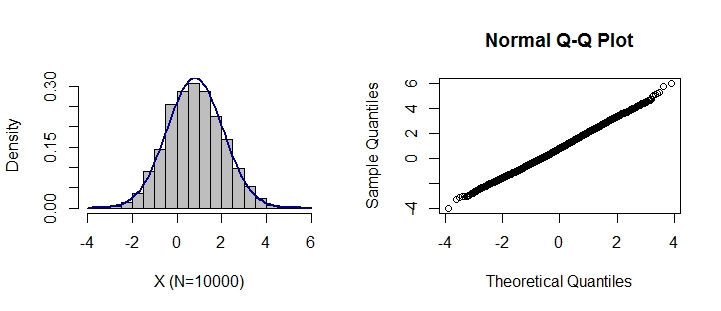
Это была присказка, а вот сказка. Я обратил внимание, что в обоих случаях использовался тест Шапиро-Уилка (Shapiro-Wilk Normality Test), и нет никакой информации о том, как ведут себя другие тесты, например, тест Колмогорова-Смирнова, хи-квадрат Пирсона и т.д. Не то, чтобы я ожидал чего-то принципиально другого, но захотелось проверить.
Для эксперимента я взял четыре распределения:
- стандартное нормальное (N(0,1))
- “почти нормальное”, описанное выше (нормальное + систематический шум)
- распределение Стьюдента с 20 степенями свободы (t(20))
- логнормальное распределение (LogN(0, 0.4)) с явной асимметрией:
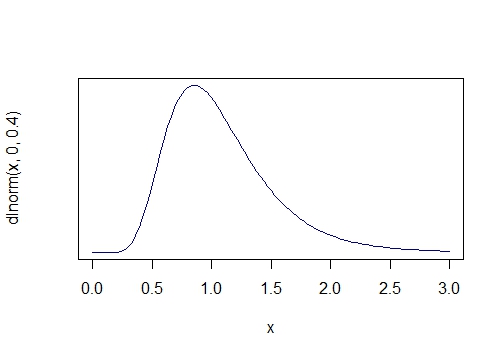
В качестве используемых тестов на нормальность взял четыре варианта:
- Критерий Шапиро-Уилка (), считающийся более подходящим для небольших выборок.
- Критерий Колмогорова-Смирнова с поправкой Лиллиефорса (Lilliefors test), который считается более подходящим для больших выборок.
- Критерий Андерсона-Дарлинга (Anderson–Darling test), свободного от распределения, то есть неспецифического для нормального распределения
- Критерий согласия Пирсона (Pearson’s chi-squared test).
С помощью каждого из этих тестов я оценил по 1000 выборок размером 10, 100, 1000 и 5000 для каждого из 4 видов распределений. Наконец, каждом таком наборе из 1000 выборок я рассчитал долю случаев, когда уровень значимости был меньше 0.05, то есть отвергалась гипотеза о нормальности.
Для интересующихся скрипт на R доступен здесь. Ему не хватает изящества, я поленился писать функции и поэтому вышло несколько громоздко, но разобраться вполне можно.
Результаты сведены в таблицах, отдельно для каждого теста, по столбцам – типы распределений, по строкам – размер выборок.
Для теста Шапиро-Уилка:
| | Normal| Almost normal| t(20)| Log-normal| |:--------|------:|-------------:|-----:|----------:| |N = 10 | 0.049| 0.038| 0.067| 0.197| |N = 100 | 0.051| 0.041| 0.114| 0.981| |N = 1000 | 0.039| 0.190| 0.417| 1.000| |N = 5000 | 0.038| 0.770| 0.952| 1.000|
Тест Лиллиефорса:
| | Normal| Almost normal| t(20)| Log-normal| |:--------|------:|-------------:|-----:|----------:| |N = 10 | 0.050| 0.049| 0.046| 0.116| |N = 100 | 0.060| 0.056| 0.073| 0.835| |N = 1000 | 0.040| 0.114| 0.130| 1.000| |N = 5000 | 0.039| 0.531| 0.479| 1.000|
Тест Андерсона-Дарлинга:
| | Normal| Almost normal| t(20)| Log-normal| |:--------|------:|-------------:|-----:|----------:| |N = 10 | 0.048| 0.048| 0.056| 0.161| |N = 100 | 0.060| 0.045| 0.090| 0.953| |N = 1000 | 0.054| 0.156| 0.246| 1.000| |N = 5000 | 0.055| 0.748| 0.834| 1.000|
Хи-квадрат Пирсона:
| | Normal| Almost normal| t(20)| Log-normal| |:--------|------:|-------------:|-----:|----------:| |N = 10 | 0.062| 0.067| 0.058| 0.130| |N = 100 | 0.046| 0.058| 0.056| 0.673| |N = 1000 | 0.044| 0.066| 0.095| 1.000| |N = 5000 | 0.065| 0.196| 0.208| 1.000|
В общем, получается, что все тесты ведут себя похоже: они, конечно, правильно “распознают” нормальное распределение при любом размере выборки, но при искажениях становятся очень зависимыми от размера выборок: на небольших выборках они слишком часто определяют распределение как нормальное, даже для явно ненормального логлинейного распределения, а на больших – практически при любом минимальном отклонении не позволяют сделать вывод о нормальности. Последнее в наименьшей степени выражено у критерия согласия Пирсона.
Вывод – проверка на нормальность с помощью тестов – дело довольно неблагодарное. Другие методы – “на глаз”, или как это названо в пересказанной мною заметке “fat pencil” test, оценка через оценку эксцесса и асимметрии – тоже не слишком однозначны. В реальных данных “чистое” нормальное распределение получается очень редко.
Возможный выход из этой ситуации мне видится следующим: сосредоточиться не на проверке нормальности, а на поведении статистик при ее нарушении, как, например, сделали мы в своей статье о применимости t-критерия и критерия Манна-Уитни в случае небольших выборок с ненормальными распределениями.