В поисках внятных объяснений про построение и смысл доверительных интервалов просматривал разнообразные материалы и убедился лишний раз, что существует одно довольно устойчивое заблуждение о содержательном смысле доверительных интервалов, которое транслируется во многих источниках.
Вот достаточно корректное определение доверительного интервала:
Другими словами, доверительный интервал обладает тем свойством, что, во-первых, его границы вычисляются исключительно по выборке (и, следовательно, не зависят от неизвестного параметра), и, во-вторых, он накрывает неизвестный параметр с вероятностью γ.
Рядом с этой ссылкой в гугле соседствует такое рассуждение:
Когда у нас есть только одна выборка, мы называем это стандартной ошибкой среднего (SEM) и вычисляем 95% доверительного интервала для среднего <... формула ...>
Если повторить этот эксперимент несколько раз, то интервал будет содержать истинное среднее популяции в 95% случаев.
Обычно это доверительный интервал как, например, интервал значений, в пределах которого с доверительной вероятностью 95% находится истинное среднее популяции (генеральное среднее).
Хотя это не вполне строго (среднее в популяции есть фиксированное значение и поэтому не может иметь вероятность, отнесённую к нему) таким образом интерпретировать доверительный интервал, но концептуально это удобнее для понимания.
Выделенный мною кусок текста содержит то самое заблуждение, о котором я говорю. Такое же определение есть в популярной и уважаемой книге А.Д. Наследова “SPSS 19. Профессиональный статистический анализ данных” (стр. 194):
95% Confidence Interval for Mean (Доверительный интервал для среднего значения в 95 %) — при большом числе выборок из генеральной совокупности 95 % средних значений этих выборок попадут в интервал, определяемый указанными в таблице границами
Это неверное рассуждение, и вот почему. Доверительный интервал, также как и любая другая выборочная оценка, зависит от выборки. И если она по каким-либо причинам смещена, то и интервал будет точно также смещен и утверждать, что он с вероятностью γ содержит истинное значение неизвестного оцениваемого параметра неверно. Допустим, мы точно знаем, что некоторый параметр равен 0, тогда в 5% случаев доверительный интервал будет “промахиваться” мимо нуля, и если мы получим такой интервал, утверждать, что истинное значение параметра лежит в этом интервале с вероятностью 95% принципиально неверно. Также ошибкой будет утверждать, что при последующих испытаниях в 95% случаев выборочные значения параметра будут попадать в этот интервал.
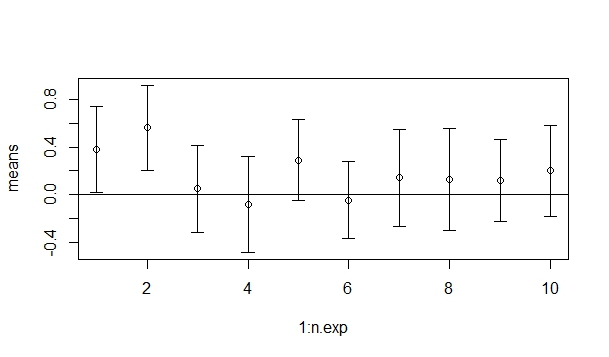
Вот, например, я смоделировал ситуацию, в которой из 10 экспериментов доверительные интервалы для случайной величины N(0,1) в двух первых выборках доверительный интервал смещен и не включает в себя ноль (для интересующихся: у меня это получилось с 1949 раза, вот скрипт на R, можно воспроизвести).
То есть, мы можем получить ошибочный результат, даже при повторном повторении эксперимента. В этом нет ничего удивительного или неожиданного, доверительный интервал – не панацея, он в нем есть те же недостатки, что и у традиционной проверки нулевой гипотезы, не стоит об этом забывать.
Хотя доверительные интервалы – это более полное описание данных, чем точечные оценки, он уводит от бинарного мышления по типу “есть различия/нет различий”, но с его интерпретацией надо быть осторожней.
В качестве бонуса, для любителей методов Монте-Карло. Скрипт вот здесь.
Я провел следующи эксперимент: 10000 сгенерировал выборку размером 100, взятую из стандартного нормального распределения N(1,0).
Для каждой из них рассчитаны и сохранены 95% доверительные интервалы среднего (которое должно соответствовать математичесому ожиданию).
Естественно, что среднее равное нулю я не получил ни разу, однако интервалы должны “накрывать” ноль примерно в 95% случаев.
Затем я рассчитал долю интервалов, находящихся выше или ниже 0.
Такой эксперимент я повторил 10 раз, результаты (доли “ошибочных” интервалов) сведены в таблице:
|Cyc| ниже 0 | выше 0 | Сумма | |--:|--------:|-------:|----------:| | 1| 0.0257| 0.0221| 0.0478| | 2| 0.0249| 0.0272| 0.0521| | 3| 0.0244| 0.0248| 0.0492| | 4| 0.0269| 0.0233| 0.0502| | 5| 0.0265| 0.0264| 0.0529| | 6| 0.0255| 0.0277| 0.0532| | 7| 0.0232| 0.0254| 0.0486| | 8| 0.0258| 0.0245| 0.0503| | 9| 0.0255| 0.0209| 0.0464| | 10| 0.0252| 0.0246| 0.0498|
Результат вполне ожидаемый, средний процент ошибок колеблется около 5 (средняя доля по всем циклам – 0.05005). В 5.005% случаев интервал промахивается мимо истинного математического ожидания.